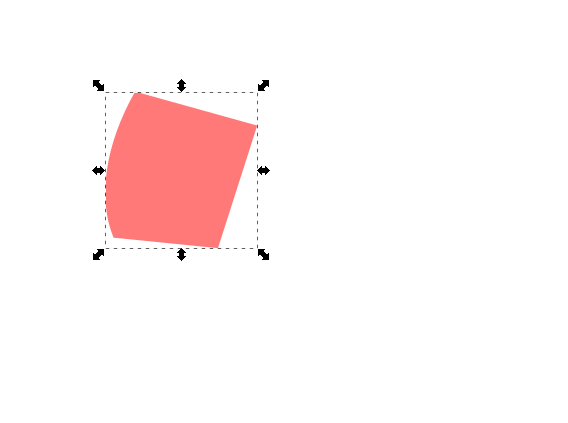
I have a problem with intersecting a bezier curve and another shape. The problem is that when I do the intersect the the left side of the intersection works fine but the right side does not. It takes the corners of the bezier curve and thinks that those belong to the other object. Here are some images to demonstrate:



Why is it acting like this?

Thanks for answers!

Please attach the original svg file, or a link to it, so we can better assist.

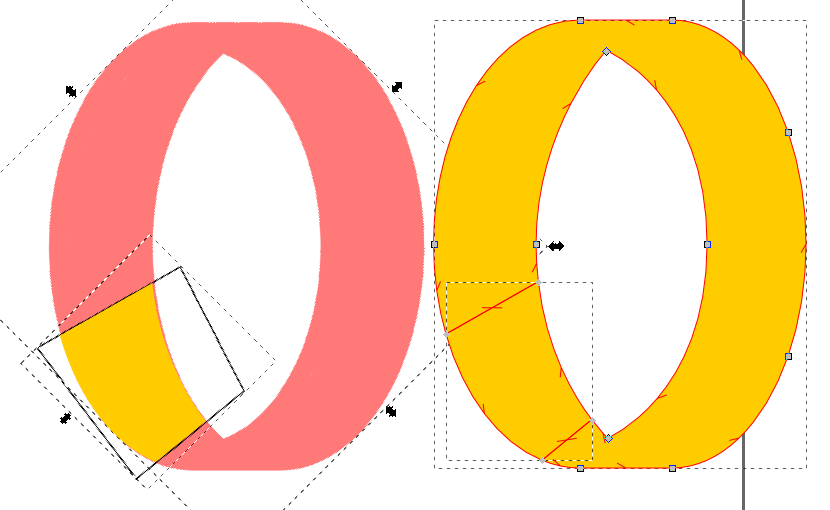
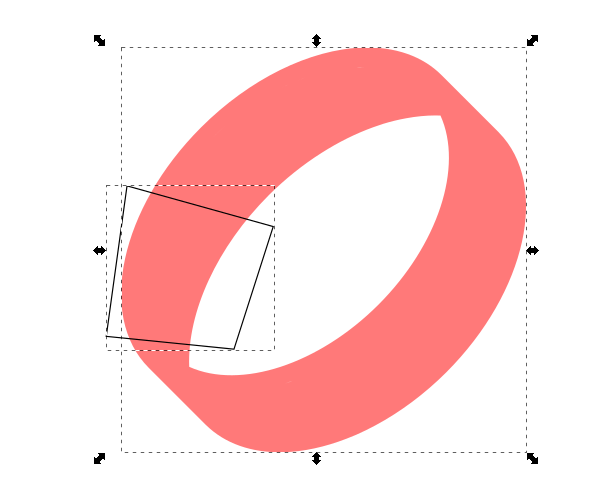
Not sure what you´re doing - but masking and division work as expected.
Can we see a node-view of the ring please?


Cheers
P.

In which order do you select the objects before intersecting?
First the ring and then the polygon or the other way round?
Try it both ways. If you see a difference it has probably something to do with the fill-rule.
Check here: (Section Fill Rule)
http://tavmjong.free.fr/INKSCAPE/MANUAL ... troke.html

Based on your question, I was interested in how intersection behaves...
Your ring shape is an object with a hole, i.e. the path actually consists out of two combined subpaths. Whether the circle appears filled or with a hole is determined by the fill rule (see the symbols in the fill dialog (Shift+Ctrl+F)), it's either even-odd (EO) or non-zero (NZ).
Furthermore, a path has a direction, let's call it here clockwise (CW) and counterclockwise (CCW).
So you end up with several options:
1. Outer circle path: CW or CCW
2. Inner circle path: CW or CCW
3. Circle ring fill: EO or NZ
4. Rectangle: CW or CCW
5. Rectangle fill: EO or NZ
6. Order of selection: Rectangle 1st or Rectangle 2nd

This gives you 2^6 = 64 possibilities which are realized in the following graph.
Blue are the original objects, green are the intersected results.
Most of the combinations result in the pattern you would expect.
Some "surprises" are the combinations: a1, a3, b2, b4, g1, g3, h2 and h4. (edit: some mistake in column g now corrected).

Certainly, there is an explanation for it. If not, it's a bug or a feature .
I guess in your case you're having one of the cases a1, a3, g1 or g3.

It is assumed that the rectangle is always on top of the circle, otherwise you will have a 7th option and 128 possibilities. Maybe there is even an influence on the order of the subpaths of the circle ring, which would be an 8th option and 256 combinations? Haven't checked yet.