Mathematical background
The golden ratio means the following:
a:b=b:(a+b)
which is equal with this:
a*(a+b)=b^2
furthermore
a^2+ab=b^2
b^2-ab-a^2=0
which results as b=(a+-(a^2+4a^2)^0.5)/2=a*(1+5^0.5)/2
thus the golden ratio can be written in a more direct form:
a:b=1:((5^0.5+1)/2),
and 1:((5^0.5+1)/2)=((5^0.5-1)/2):(((5^0.5-1)/2)*(5^0.5+1)/2)=(5^0.5-1)/2:1
-which makes the connection to Fibonacci.
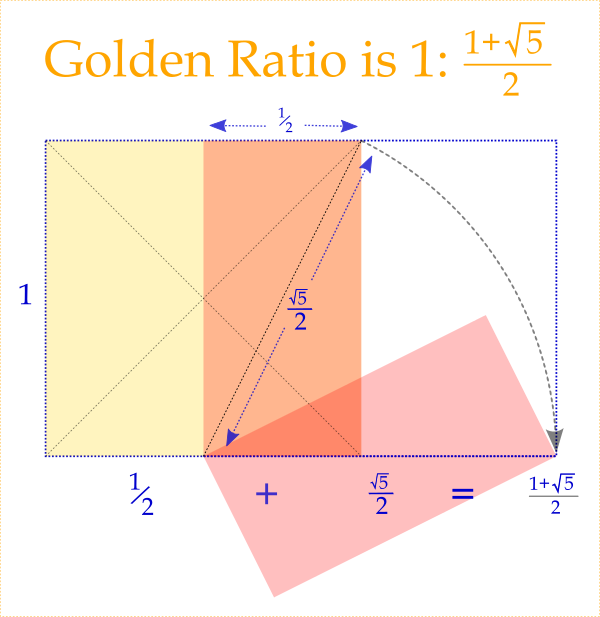
To construct the golden ratio, we will have to draw this (5^0.5-1)/2 ration.
We will use a right-angled triangle which has a leg double times longer than the other.
The ratio between the sides will be then 1:5^0.5:2 by Pytahgoras theorem, this is what the construction uses.
If the shorter leg's length is subtracted from the hypotenuse, it will make the golden ratio with the longer leg.
Here are the steps how it looks like all in inkscape:



















It might not be simpe or fast if you doing it for the first time -or if you making a tutorial of it...-, but
it doesn't take much more time than opening the calculator from the accessories, typing in ((5^0.5)+1)/2 and multiply it with the smaller size of a rectangle, to get the longer size's correct width, that you type in to have the same result as with the construction method.
 This is a read-only archive of the inkscapeforum.com site. You can search for info here or post new questions and comments at
This is a read-only archive of the inkscapeforum.com site. You can search for info here or post new questions and comments at 
 And look, he managed to post them before I could even post!
And look, he managed to post them before I could even post!